How bits work
You’ve likely heard before that PCs store things in 1s and 0s. These major units of data are known as pieces. At the point when a piece is “on,” it compares with a 1; when it’s “off,” it transforms into a 0. Each piece, at the end of the day, can store just two bits of information.
But once you string them together, the measure of data you can encode develops dramatically. Two pieces can speak to four snippets of data in light of the fact that there are 2^2 mixes: 00, 01, 10, and 11. Four pieces can speak to 2^4, or 16 snippets of data. Eight pieces can speak to 2^8, or 256. Thus on.
The right blend of pieces can speak to sorts of information like numbers, letters, and tones, or kinds of tasks like expansion, deduction, and correlation. Most workstations these days are 32-or 64-digit PCs. That doesn’t mean the PC can just encode 2^32 or 2^64 snippets of data all out. (That would be a weak PC.) It implies that it can utilize that numerous pieces of unpredictability to encode each bit of information or individual operation.
4-digit profound learning
So what does 4-bit preparing mean? All things considered, to begin, we have a 4-digit PC, and accordingly 4 pieces of multifaceted nature. One approach to consider this: each and every number we use during the preparation cycle must be one of 16 entire numbers between – 8 and 7, on the grounds that these are the main numbers our PC can speak to. That goes for the information focuses we feed into the neural organization, the numbers we use to speak to the neural organization, and the transitional numbers we need to store during training.
So how would we do this? We should initially consider the preparation information. Envision it’s an entire bundle of high contrast pictures. Stage one: we need to change over those pictures into numbers, so the PC can get them. We do this by speaking to every pixel as far as its grayscale esteem—0 for dark, 1 for white, and the decimals between for the shades of dim. Our picture is presently a rundown of numbers going from 0 to 1. Yet, in 4-cycle land, we need it to go from – 8 to 7. The stunt here is to straightly scale our rundown of numbers, so 0 becomes – 8 and 1 gets 7, and the decimals guide to the whole numbers in the center. So:
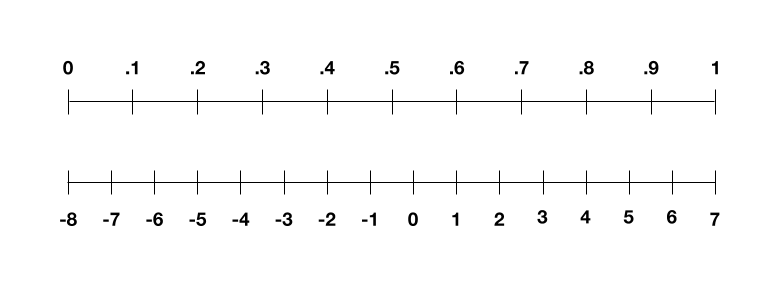You can scale your rundown of numbers from 0 to 1 to extend between – 8 and 7, and afterward round any decimals to an entire number.
This measure isn’t awesome. On the off chance that you began with the number 0.3, state, you would wind up with the scaled number – 3.5. Be that as it may, our four pieces can just speak to entire numbers, so you need to adjust – 3.5 to – 4. You wind up losing a portion of the dim shades, or supposed exactness, in your picture. You can perceive what that resembles in the picture below.
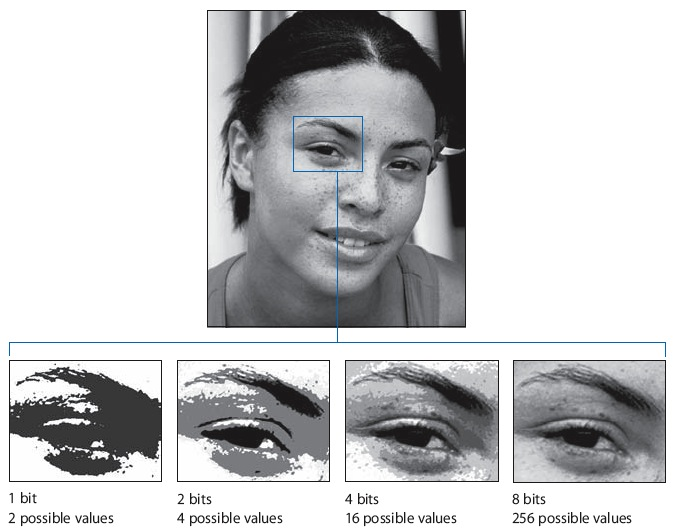The bring down the quantity of pieces, the less detail the photograph has. This is what is known as a deficiency of exactness.
This stunt isn’t excessively pitiful for the preparation information. However, when we apply it again to the neural organization itself, things get a smidgen more complicated.
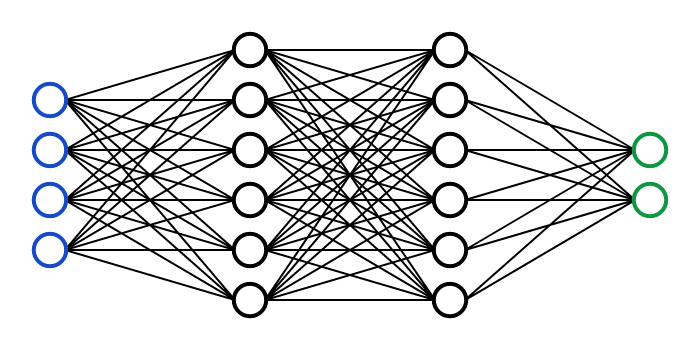A neural organization.
We regularly observe neural organizations drawn as something with hubs and associations, similar to the picture above. Be that as it may, to a PC, these likewise transform into a progression of numbers. Every hub has a supposed enactment esteem, which typically goes from 0 to 1, and every association has a weight, which for the most part goes from – 1 to 1.
We could scale these similarly we did with our pixels, yet initiations and loads additionally change with each round of preparing. For instance, now and again the enactments range from 0.2 to 0.9 in one round and 0.1 to 0.7 in another. So the IBM bunch sorted out another stunt in 2018: to rescale those reaches to extend between – 8 and 7 in each round (as demonstrated as follows), which viably tries not to lose an excess of precision.
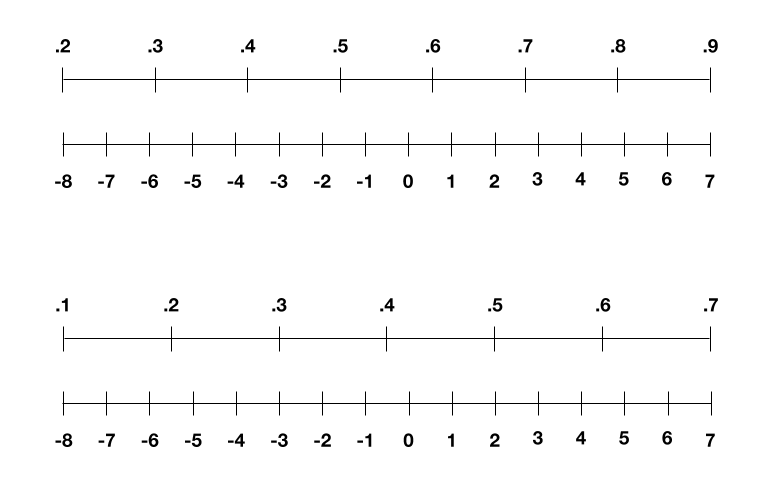The IBM specialists rescale the actuations and loads in the neural organization for each round of preparing, to try not to lose a lot of exactness.
But then we’re left with one last piece: how to speak to in four pieces the halfway qualities that yield up during preparing. Challenging that these qualities can length over a few significant degrees, not at all like the numbers we were taking care of for our pictures, loads, and initiations. They can be small, as 0.001, or colossal, as 1,000. Attempting to straightly scale this to between – 8 and 7 loses all the granularity at the little finish of the scale.
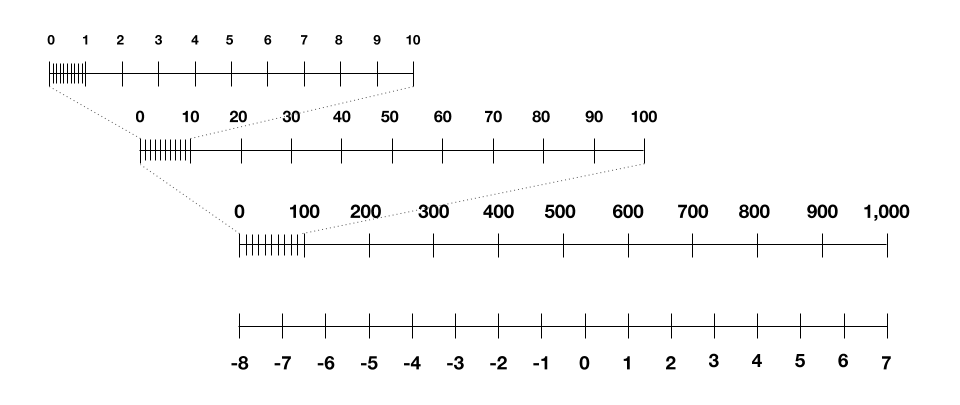Linearly scaling numbers that range a few significant degrees loses all the granularity at the small finish of the scale. As should be obvious here, any numbers more modest than 100 would be scaled to – 8 or – 7. The absence of accuracy would hurt the last execution of the AI model.
After two years of exploration, the scientists at last broke the riddle: acquiring a current thought from others, they scale these middle of the road numbers logarithmically. To perceive what I mean, beneath is a logarithmic scale you may perceive, with a supposed “base” of 10, utilizing just four pieces of multifaceted nature. (The scientists rather utilize a base of 4, since experimentation demonstrated that this worked best.) You can perceive how it allows you to encode both small and huge numbers inside the touch constraints.
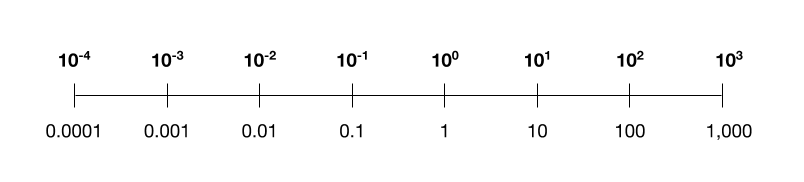A logarithmic scale with base 10.
With every one of these pieces set up, this most recent paper shows how they meet up. The IBM specialists run a few analyses where they reenact 4-digit preparing for an assortment of profound learning models in PC vision, discourse, and normal language handling. The outcomes show a restricted loss of precision in the models’ general execution contrasted and 16-bit profound learning. The cycle is likewise in excess of multiple times quicker and multiple times more energy efficient.
